Wie groß ist der Einfluss des Zufalls im Fußball?
Wir wollen einen Versuch unternehmen, um die Bedeutung des Zufalls im Fußball zu quantifizieren. Dies ist ein äußerst schwieriges Unterfangen und viele denkbare Zugänge sind möglich. Der Zufall spielt eine deutlich größere Rolle, als der gemeine Fußballfan wohl vermuten würde. Simuliert man eine Liga gleich starker Mannschaften mit realistischen Zufallsergebnissen, so beträgt der Punktunterschied zwischen dem ersten und letzten der Liga etwa 30 Punkte (A. Werner, MDMV 19, 2011)! Jedoch mischt sich die zufällige Komponente eben auch mit dem Einfluss der Qualität der Spieler. Dies auseinander zu halten ist eine mehr als schwierige Aufgabe.
Wie könnte man den Zufall quantifizieren? Wir versuchen dies anhand von knappen Spielen zu tun. Die Frage ist nur, was ist ein knappes Spiel? Unsere Definition eines knappen Spiels wird über die Torchancen-Differenz formuliert, für letztere Größe verwenden wir xGoals. Die Idee hinter diesem Vorgehen ist die, dass bei etwa gleichen Torchancen vornehmlich der Zufall entscheidet, ob eine gegebene Torchance in ein Tor verwandelt wird. Selbstverständlich entscheidet nicht nur der Zufall, ob eine Torchance zu einem Tor führt, sondern eben auch die Qualität des Schützen und die des Torwartes. Mittelt man über alle solche Torchancen, wird eine Abweichung von dem idealen Mittelwert unter Umständen eine Aussage ermöglichen, wie groß in etwa der Anteil des Zufalls im Vergleich zur Spieler-Qualität ist. Zumindest ist dies die Hoffnung!
Definition eines knappen Spiels
Wir definieren ein knappes Spiel $s$ über die xGoal-Differenz:
$$
dG(s) := | xG_H(s) - xG_G(s) | < d
$$
wobei $xG_H(s)$ und $xG_G(s)$ die xGoal-Werte des Spiels $s$ der Heim- und Gast-Mannschaft ist und die Größe $d$ ein noch zu definierender Wert ist. Die genaue Wahl stellt offenbar eine gewisse Willkür in der Definition dar. Desto niedriger $d$ gewählt wird, desto größer spielt der Zufall eine Rolle, jedoch werden die Anzahl der Spiele die zur Statistik beitragen geringer. Vergrößert man $d$, so steigt die Anzahl der Spiele in der Statistik, aber der Zufall hat dann einen immer geringeren Einfluss, da es sich immer weniger um ein knappes Spiel handelt. Natürliche Wahlen wären etwa $d=0.5, 0.75$ oder $1$. Wir entscheiden uns hier für den Mittelweg von $d=0.75$, was nebenbei bemerkt dem xG-Wert für die Torchance bei einem Elfmeter entspricht und somit eine anschauliche Vorstellung dafür liefert.
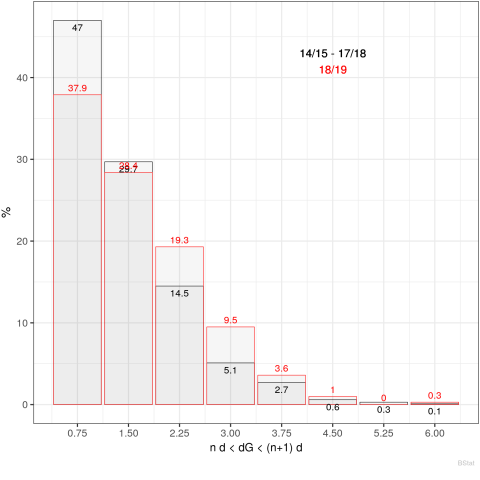
Schauen wir uns die 4 Spielzeiten 14/15-17/18 an, so gab es 575 knappe Spiele (mit $d=0.75$), was einem Anteil von 47% aller $S=1224$ Spiele entspricht. Gruppiert in Abschnitte $n\cdot d < dG < (n+1)\cdot d,\; n=0,1...,7$ ist die Verteilung in der folgenden Grafik dargestellt. Als Vergleich sind die entsprechenden Daten der Saison 2018/19 in Rot eingezeichnet. Etwas weniger als die Hälfte aller Spiele in einer Saison sind demnach knappe Spiele.
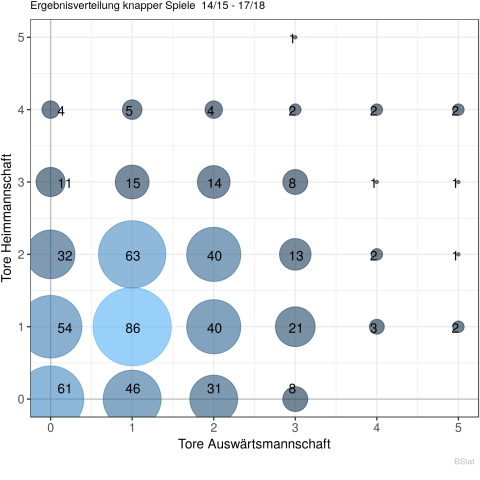
Für eine andere Wahl mit $d=0.5$ sind es 34% der Spiele und für $d=1$ sind es 58% knappe Spiele. Der letztere Wert ist deutlich zu hoch, der erstere Wert wäre eventuell besser, aber der statistische Fehler für eine einzelne Saison ist zu hoch, wie wir im Verlauf der Diskussion noch sehen werden. Betrachten wir die Ergebnisverteilung aller knappen Spiele in der nachfolgenden Grafik, so erkennen wir, dass auch tatsächlich die überwiegende Mehrzahl aller knappen Spiele definiert über $dG(s)<0.75$ tatsächlich auch ein knappes Spielergebnis zur Folge hatte.
Nehmen wir also im Folgenden die so definierten knappen Spiele als Basis unserer Untersuchung und schauen im nächsten Abschnitt an, wie gleich verteilt die Spielausgänge sind.
Punkteverteilung der knappen Spiele 14/15-17/18
Ein wichtiges Indiz für eine gute Wahl des Parameters $d$ ist die Punkteverteilung der knappen Spiele. Wäre diese ideal (infinitesimal kleines $d$ und eine sehr große Anzahl von Spielen $S$), dann wären alle drei Ergebnisse aus Sicht der Heimmannschaft [Sieg (S), Unentschieden (U) und Niederlage (N)] gleich wahrscheinlich. Da aber ein Heimvorteil in allen Ligen existiert, gibt es keine Gleichverteilung der Ergebnisse, sondern eine Verschiebung hin zu Heimsiegen. Im Konkreten sieht die Anteils-Verteilung $P$ der Spielausgänge für die betrachteten 4 Spielzeiten wie folgt aus:
$$
P_S = 0.356, \qquad P_U=0.342, \qquad P_N=0.301.
$$
Diese Werte weichen damit tatsächlich nicht sehr vom idealen Wert $P=1/3$ ab, zeigen aber schon die angesprochene Tendenz zu Heimsiegen! Korrekterweise müssten wir im Folgenden mit diesen Schätzern $P_S, P_U$ und $P_N$ der Wahrscheinlichkeiten rechnen. Um die Interpretation und folgende Argumentation etwas zu vereinfachen, nehmen wir der einfachheitshalber $P=1/3$ an. Dann ist der theoretische Erwartungswert der Punktzahl über alle Spiele:
$$
\bar{p}=\sum_{s=1}^S p(s)\frac{P(s)}{S} = \frac{1}{S}\big(3P_S +P_U\big),
$$
dabei ist $p(s)=3,1,0$ die Punktzahl im Spiel $s$, für Sieg, Unentschieden und Niederlage. Die Summe geht über alle knappen Spiele, in unserem Fall über $S=575$ Spiele. Bei Verwendung der idealen Verteilung ergibt sich $\bar{p}=4/3=1.333...$, im Vergleich zu $\bar{p}=1.41$ bei Verwendung der Schätzer. Der Fehler durch diese Vereinfachung der Betrachtung ist damit klein.
Die verschiedenen Mannschaften werden in Summe unterschiedliche Anzahl von knappen Spielen aufweisen, um diese einheitlich vergleichen zu können definieren wir im nächsten Abschnitt die Punkteausbeute.
Punkteausbeute als Erfolgsmaß
Zum Vergleich des Erfolgs von Mannschaften in $S$ knappen Spielen, werden wir die Punkteausbeute $p_{100}(S)$ jeder Mannschaft auf die maximal mögliche Anzahl von Punkten normieren, die in $S$ knappen spielen möglich gewesen wäre, und geben diese in Prozent an:
$$
p_{100}(S) := \frac{100}{3S} \sum_{s=1}^S p(s).
$$
Demnach entspricht der Erwartungswert $\bar{p}=4/3$ einem $p_{100}=100/3S \cdot S4/3 =44.4...$. Das ist der Erfolgswert, den durchschnittlich ein Team zu erwarten hätte, wenn alle Spielausgänge zufällig gewesen wären. Selbstverständlich bedeutet dies nicht, dass jede Mannschaft genau diese mittlere Erfolgsquote hat, denn der Zufall sorgt eben dafür, dass es Schwankungen gibt. Diese Schwankung lässt sich abschätzen, hierauf wollen wir im Detail nicht eingehen, aber anmerken, dass diese Grenzen in den folgenden Diagrammen als rote vertikale Linien neben der grauen Erwartungswertlinie mit eingezeichnet werden.
Aufgrund der größeren Datenbasis und als Vergleichsmaßstab für die laufende Saison schauen wir uns zunächst die Punkteausbeute der knappen Spiele der vergangenen Saison an.
Knappe Spiele 17/18
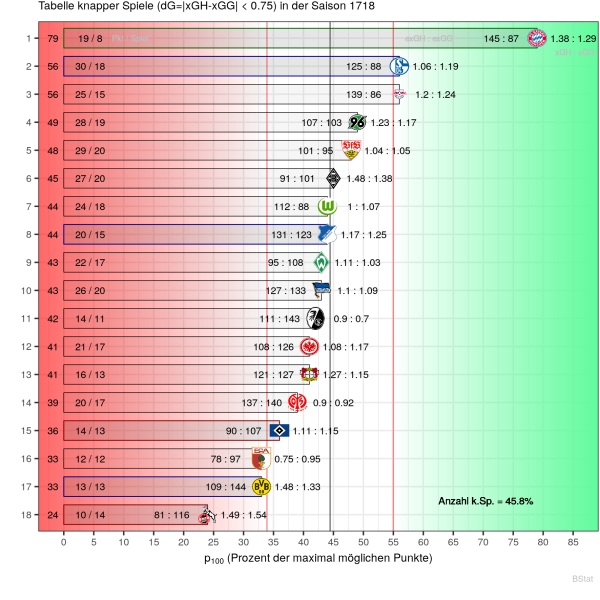
Die Anzahl der knappen in der Saison 17/18 lag bei 45.8%, also sehr nahe am Vierjahresmittel. Die folgende Grafik zeigt die Tabelle der normierten Punkteausbeute $p_{100}$. Zusätzlich sind die Punkte und Spiele (Pkt/Spiel), die Effizienz in Tore pro $xG_H$ bzw Tore pro $xG_G$ in Prozent (exGH:exGG) und das mittlere xGoal-Ergebnis pro Spiel (xGH:xGG) je Mannschaft angegeben. Der #FCB fällt nicht nur in der Punkteausbeute aus dem Rahmen, auch in der Anzahl der knappen Spiele, die mit Abstand am geringsten ausfällt. Die Anzahl der knappen Spiele ist darüber hinaus über alle Teams unauffällig zwischen 13 und 20 Spiele verteilt.
Zunächst ein paar allgemeine Bemerkungen zur Grafik. Der Meister ist in Grün, die Champions League Plätze in Blau und die Absteiger sind in Rot gekennzeichnet. Im Sinne unserer Ausgangsfragestellung ist es wichtig an dieser Stelle zu bemerken, dass die Schwankung sehr groß ist. Lediglich 2 Teams (#FCB und #KOE) liegen deutlich außerhalb der Schwankung, jeweils im positiven wie im negativen Sinne. Vier weitere Teams liegen an der Grenze, #S04 und #RBL im Positiven und #FCA und #BVB im Negativen. Die allermeisten Teams liegen tatsächlich um den erwarteten Wert von $\bar{p}=44.4...$. Für diese Teams könnte man sagen, alles ist statistisch recht normal verlaufen. Allenfalls könnte man im Detail in der Effizienz bzw des xGoals-Ergebnisses nach Auffälligkeiten suchen. Dies wollen wir an dieser Stelle nicht verfolgen, da zur Interpretation oft ein Detailwissen zur jeweiligen Mannschaft nötig ist. Gehen wir stattdessen über zu den Auffälligkeiten der Teams, die außerhalb der Schwankung liegen.
Knappe Spiele 18/19
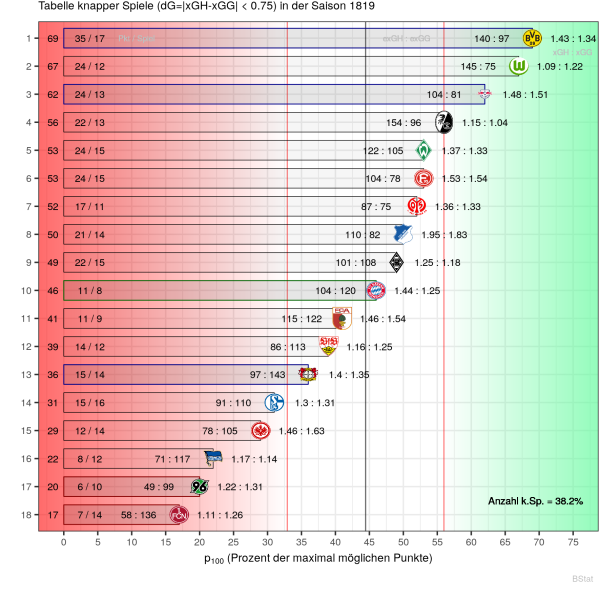
Die Zahl der knappen Spiele liegt mit 38.2 leicht aber nicht signifikant unter dem Schnitt der letzten 4 Jahre. Im Vergleich zur Saison 2017/18 gibt es mehr Teams, die außerhalb der Schwankung liegen. Zwischen den Plätzen 4 und 14 ist statistisch alles normal und sollte nicht interpretiert werden. Ein Spiel mehr oder weniger gewonnen und verloren kann hier gut 3-4 Plätze in der Rangliste ausmachen. Deswegen werden in der Team-Analyse nur die Teams betrachtet, die deutlich außerhalb der Schwankung liegen.
Team-Analysen
![]() Der BVB liegt in der Punkteausbeute mit 69% an der Spitze und hat die meisten knappen Spiele aller Teams absolviert! Das gute Ergebnis ist in erster Linie durch die Offensive begründet, die 40% mehr Tore erzielt hat als nach den xGoals zu erwarten gewesen wären. In der Defensive sind genau so viele Tore gefallen, wie zu erwarten waren.
Der BVB liegt in der Punkteausbeute mit 69% an der Spitze und hat die meisten knappen Spiele aller Teams absolviert! Das gute Ergebnis ist in erster Linie durch die Offensive begründet, die 40% mehr Tore erzielt hat als nach den xGoals zu erwarten gewesen wären. In der Defensive sind genau so viele Tore gefallen, wie zu erwarten waren.
![]() Die Wolfsburger auf Platz 2 sind in der Offensive noch eine Idee effizienter gewesen aber auch in der Defensive mit 75% (exGG) das glücklichste Team der Saison. Des Weiteren haben die Wolfsburger in den knappen Spielen die geringste xGoals (1.09 xGH) aller Teams aufzuweisen.
Die Wolfsburger auf Platz 2 sind in der Offensive noch eine Idee effizienter gewesen aber auch in der Defensive mit 75% (exGG) das glücklichste Team der Saison. Des Weiteren haben die Wolfsburger in den knappen Spielen die geringste xGoals (1.09 xGH) aller Teams aufzuweisen.
![]() RB Leipzig auf Platz 3 profitiert in allererster Linie von der Defensive bei sonst ausgeglichen Daten.
RB Leipzig auf Platz 3 profitiert in allererster Linie von der Defensive bei sonst ausgeglichen Daten.
![]() Platz 15 für die Eintracht ist durch die mangelnde offensive Effizienz (78%) in knappen Spielen begründet. Berücksichtigt man die Qualität der Offensive, ist hier vielleicht eher das fehlende Glück die Ursache.
Platz 15 für die Eintracht ist durch die mangelnde offensive Effizienz (78%) in knappen Spielen begründet. Berücksichtigt man die Qualität der Offensive, ist hier vielleicht eher das fehlende Glück die Ursache.
![]() Die Hertha war, bei praktisch ausgeglichenen xGoals, sowohl offensiv (71%) als auch defensiv (117%) ineffizient.
Die Hertha war, bei praktisch ausgeglichenen xGoals, sowohl offensiv (71%) als auch defensiv (117%) ineffizient.
![]() Mit der schlechtesten offensiven Effizienz von 49% ist der schlechte Platz in der Rangliste und Saisonabschlusstabelle eindeutig der Offensive anzukreiden.
Mit der schlechtesten offensiven Effizienz von 49% ist der schlechte Platz in der Rangliste und Saisonabschlusstabelle eindeutig der Offensive anzukreiden.
![]() Die Daten für die Nürnberger sind desolat. Vorne wurde nichts getroffen und hinten viel gefangen. Zusammen kann das nicht gut gehen und ist dann vermutlich nicht nur fehlendes Glück.
Die Daten für die Nürnberger sind desolat. Vorne wurde nichts getroffen und hinten viel gefangen. Zusammen kann das nicht gut gehen und ist dann vermutlich nicht nur fehlendes Glück.
Weitere Interpretationen wollen wir den Vereinsexperten überlassen und kommen zu einem kleinen Fazit.
Fazit
Die ursprünglich gestellte Frage nach der Bedeutung des Zufalls lässt sich leider nur in Teilen beantworten und bestätigt eher bekanntes Fußballallgemeinwissen. Der Zufall spielt im Fußball durch die geringe Anzahl von Toren in einem Spiel, wie in keiner anderen Ballsportart, eine extrem große Rolle. Knappe Spiele, in denen tatsächlich eben oft der Zufall über den Ausgang entscheidet, können am Ende der Saison zur Folge haben, dass eine Mannschaft 4-8 Punkte mehr oder weniger hat, aus rein statistischen Gründen. Diese wenigen Punkte können jedoch den Unterschied zu CL vs EL oder Abstieg und Relegation bedeuten.
Die Wahl der Größe $d=0.75$ ist willkürlich, eine andere Wahl kann die Rangfolge im Bereich der Schwankung um 3-5 Plätze bedeuten. Außerhalb der Schwankung sind die Veränderungen dagegen geringer.
Ohne die Kenntnisse der Teams ist sicher nicht zu entscheiden, ob es Glück oder Pech bzw Effizienz oder Ineffizienz war, welches für den Erfolg oder Misserfolg maßgeblich waren. Fußball!
Diskussion