How important is a successful start into the season?
What we like to address in this article is the question: What could be followed from the first games for a season final score in soccer?
First of all, this article is not a scientific analysis, it is more a collection of some selected results of recent years in the Premier League and the 1.Bundesliga. This alone is already a subjective selection, and furthermore, I will restrict the data to the years 2000-2017, which is as well a kind of arbitrariness. Secondly, I will not justify each statement individually on a statistically sound basis, but at least I will give some evidence for the claims I state. We start with a small introduction to basic terminology.
The basic data
In particular we compare the team ranking of a league during the season match days to the final ranking. Assume we have a league with $M$ teams, and let us denote the ranking of team $m\in\{1,2,...,M\}$ on match day $n\in\{1,2,...,2(M-1)\}$ by $\mathsf{rg}_n(m)\in\{1,2,...,M\}$ and the final ranking $\mathsf{rg}_{e}(m)\equiv\mathsf{rg}_{2(M-1)}(m)$ of team $m$ at the end of the season on match day $e=2(M-1)$.
Rank Correlation
The Spearman's rank correlation coefficient (in German) for match day $n$ to $e$ is given by: $$ r(n) := 1 - \frac{6}{M(M^2-1)}\sum_m\big(\mathsf{rg}_n(m)-\mathsf{rg}_e(m)\big)^2, $$ where we for simplicity have assumed that all rankings are different from each other $\mathsf{rg}_{n}(m)\neq \mathsf{rg}_{n}(m'),\; m\neq m'$. The correlation coefficient $r$ is the common measure for quantifying dependencies between two rankings. But for interpretation of a specific ranking there is a better measure, know as the Mean Absolute Error.
Mean Absolute Error
The mean absolute error for the team ranking of match day $n$ to $e$ is defined as: $$ a(n) := \frac{1}{M}\sum_m \Big| \mathsf{rg}_n(m)-\mathsf{rg}_e(m)\Big|. $$ The interpretation is very natural, it is the average distance from the final result, and it holds $a(e)=0$ and $0 \leq a(n) \leq M/2$.
Premier League
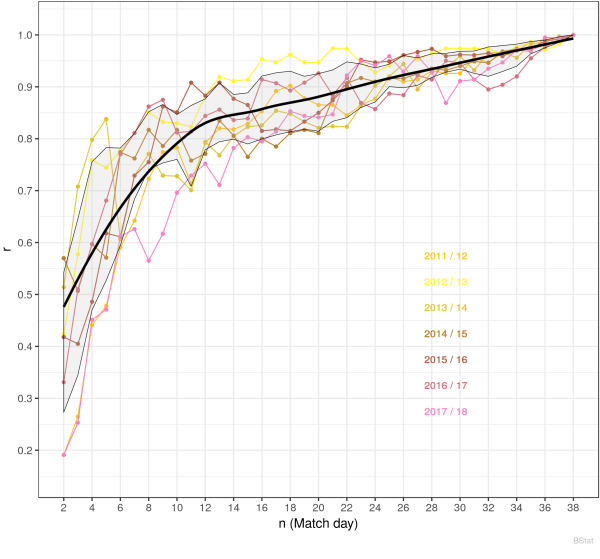
To keep track of the data, let us start with the recent 7 Premier League years (2011/12- 2017/18) and firstly look into the rank correlation $r(n)$, which is show for each season (colored thin lines) in the chart below.
The gray shaded area surrounded by thin black lines marks the standard deviation for every match day for these 7 seasons and gives a rough estimation of the fluctuation. The thick black lines is a guide to the smoothed average of the ranking $\langle \mathsf{rg}_n \rangle$. In this chart everything looks pretty stochastically and no significantly deviations outside the shaded area are observed. Note, there must be data points outside the region, otherwise something is wrong! Furthermore, an analysis of the significance level shows that the correlations are significant from match day 4-6 onward.
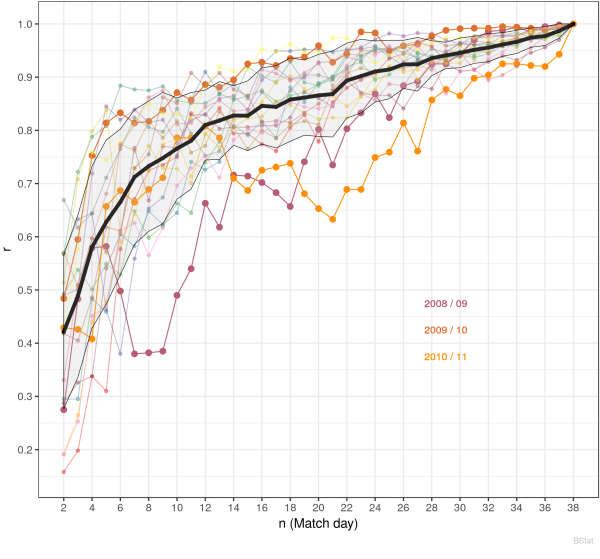
But let us now turn to the complete data set of seasons 2000/01 -2017/18, i.e. 18 years, which are shown in the following chart.
The thick black line is now the average ranking $\langle \mathsf{rg}_n \rangle$ for all years and not the smoothened one. Despite from this small difference, everything is the same as in the chart above. But now we observe at least 2 deviations, which seems not to fit into the scheme, the years 2008/09 and 2009/10-11. In particular, 2008/09 has large deviations towards lower correlations till mid season and the 2010/11 deviations starting from mid season. But it is hard to decide how statistically significant these deviations are, because the $\mathsf{rg}_n(m)$ are highly correlated.
Mean Absolute Error
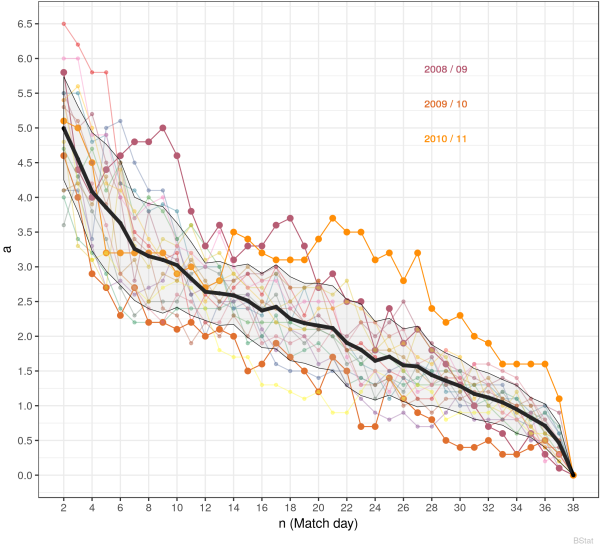
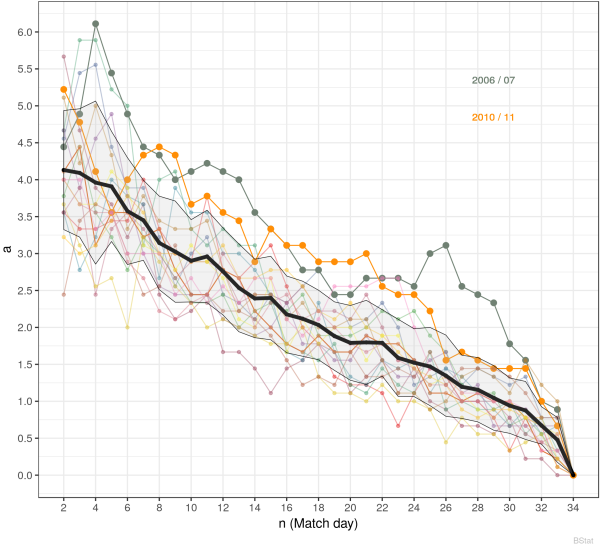
The following chart shows the mean absolute error $a(n)$ for the Premier League for 2000/01 - 2017/18. Again, the shaded area marks the individuell standard deviations of every match day for all years. Obviously, the same deviations must be observed as for the rank correlation $r(n)$.
Excluding the first 5 and last 3 match days, this is a roughly linear decrease in the absolute mean error from roughly 3.5 to 0.8.
Let us compare the Premier League to 1.Bundesliga.
Bundesliga
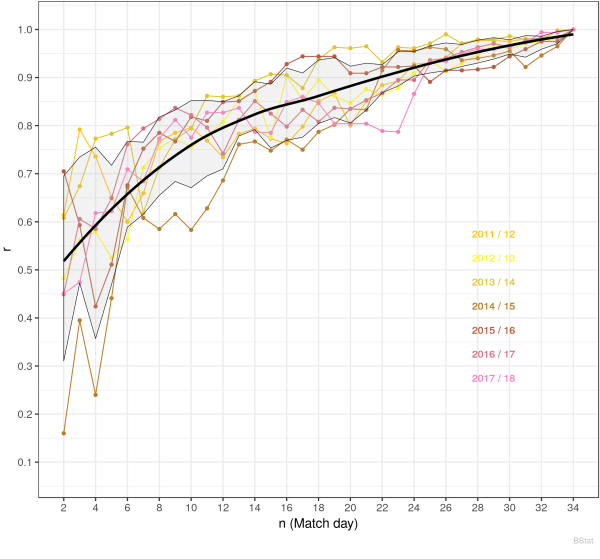
The analogous chart to the first is shown below. Everything is pretty the same, again with no statistically significant deviations and no statistically significant deviation among the leagues.
Therefore, we skip the rank correlation chart and go directly to the mean absolute error $a(n)$ for the 1.Bundesliga for 2000/01 - 2017/18. Again, we observe seasons with larger deviations. But the same holds for the conclusions, as stated for Premiere League.
Be careful!
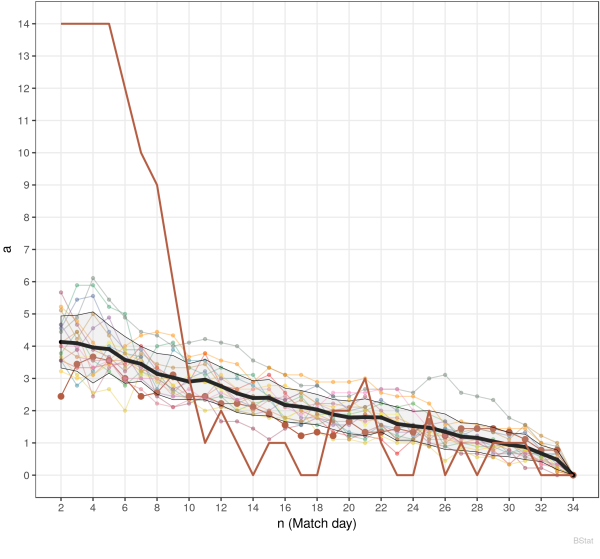
But what does this all mean for individual clubs? As always, these are all statistically statements and averages with the usual interpretations for deviations. The largest deviation within over 50 years of Bundesliga is given by Borussia Mönchengladbach in the season 2015/16. In the first 5 match days they have not scored a single point and were ranked last. Till the end of the season they made it up to rank 4, which has never been achieved - before and after - by any other team, which hast lost the first 5 games. So, this is a really extreme example, for what could happen.
The individual absolute deviation for Borussia (bmg) ($|\mathsf{rg}_{bmg}(n)-\mathsf{rg}_{bmg}(34)|$) is shown as the single thick brown curve. The corresponding season is marked with larger dots and the same color. As you can see, the large deviation for Borussia does not influence the overall graph for the season. So, large deviations for single teams may always occur.
Conclusion
So what is the answer of the introductory question? I will made it as short as possible. There is a statistically high correlation of the league ranking after match day 4-7 to the final ranking, but individuell deviations for single clubs can largely deviate, despite that the probability for such a deviation is rather small.
Diskussion
https://www.yeezyadidas.de/ Yeezy https://www.yeezys.co/ Yeezys https://www.jordan-1.org/ Jordan 1 https://www.air-jordan1.com/ Air Jordan 1 https://www.nikejordan1.com/ Nike Jordan 1 https://www.jordan-1s.com/ Jordan 1S https://www.jordan1.uk.com/ Jordan 1 https://www.jordans-shoes.com/ Jordan Shoes https://www.jordan-shoes.us.com/ Jordan Shoes https://www.nikeuk.uk.com/ Nike UK https://www.yeezy-450.com/ Yeezy 450 https://www.jordanretro4.com/ Jordan Retro 4 https://www.nikeoutletstoreonlineshopping.us/ Nike Outlet Store Online Shopping https://www.yeezy.uk.com/ YEEZY https://www.adidasyeezyofficialwebsite.com/ Adidas Yeezy Official Website https://www.yeezy350.uk.com/ Yeezy 350 https://www.air-jordan4.com/ Air Jordan 4 https://www.yeezyfoam-runner.com/ Yeezy Foam Runner https://www.yeezyslides.us.com/ Yeezy Slides https://www.ray-ban-glasses.us.com/ Ray Ban Glasses https://www.adidasuk.uk.com/ Adidas UK https://www.nflshopofficialonlinestore.com/ NFL Shop Official Online Store https://www.yeezys-slides.us.com/ Yeezy Slides https://www.yeezyadidass.us.com/ Adidas Yeezy https://www.350yeezy.us.com/ Yeezy 350 https://www.yeezyy.us.com/ Yeezy https://www.yeezy350s.us.com/ Yeezy 350 https://www.shoesyeezys.us.com/ Yeezy Shoes https://www.yeezys.uk.com/ Yeezys https://www.off-white.us.org/ Off White https://www.raybansales.us/ Ray Ban https://www.adidasyeezy.uk.com/ Adidas Yeezy https://www.yzyshoes.us.com/ Yeezy Shoes https://www.yeezy-shoes.us.com/ Yeezy Shoes https://www.yeezy-700.us.com/ Yeezy 700 https://www.yeezyadidas.de/ Adidas Yeezy https://www.yeezys.co/ Yeezy https://www.jordan-1.org/ Nike Jordan 1 https://www.air-jordan1.com/ Jordan 1 https://www.nikejordan1.com/ Jordan 1 https://www.jordan-1s.com/ Jordan 1 https://www.jordan1.uk.com/ Jordan UK https://www.jordans-shoes.com/ Jordans Shoes https://www.jordan-shoes.us.com/ Jordan https://www.nikeuk.uk.com/ Nike https://www.yeezy-450.com/ Yeezy https://www.jordanretro4.com/ Jordan 4 https://www.nikeoutletstoreonlineshopping.us/ Nike Outlet https://www.yeezy.uk.com/ YEEZY UK https://www.adidasyeezyofficialwebsite.com/ Adidas Yeezy https://www.yeezy350.uk.com/ Yeezy uk https://www.air-jordan4.com/ Jordan 4 https://www.yeezy-supply.com/ Yeezys Supply https://www.yeezyfoam-runner.com/ Yeezy https://www.yeezyslides.us.com/ YEEZY https://www.ray-ban-glasses.us.com/ Ray Bans Sunglasses https://www.adidasuk.uk.com/ Adidas https://www.nflshopofficialonlinestore.com/ NFL Shop https://www.yeezys-slides.us.com/ Yeezys https://www.yeezyadidass.us.com/ Adidas Yeezys https://www.350yeezy.us.com/ Yeezy 350 V2 https://www.yeezyy.us.com/ Yeezys https://www.yeezy350s.us.com/ Yeezy Boost 350 https://www.shoesyeezys.us.com/ Yeezys Shoes https://www.yeezys.uk.com/ Yeezy https://www.raybansales.us/ Ray Bans https://www.yeezys-supply.com/ Yeezy Supply https://www.adidasyeezy.uk.com/ Yeezy https://www.yzyshoes.us.com/ Yeezys https://www.yeezy-slides.org/ Adidas Yeezy Slides https://www.yeezy-shoes.us.com/ Yeezy https://www.yeezy-700.us.com/ Yeezy https://www.cheapyeezysonline.com/ Cheap Yeezys https://www.yeezysupplystore.com/ Yeezy Supply https://www.yeezyshoesonline.com/ Yeezy Shoes https://www.yeezys-supply.us.com/ Yeezy Supply https://www.yeezys-supply.us.com/ Yeezys https://www.yeezy-s.com/ Yeezy Shoes https://www.yeezy-s.us/ Yeezy https://www.yeezysale.us/ Yeezy https://www.pandorajewelries.us.com/ Pandora Jewelry Tags:yeezy shoes, Yeezy, Adidas Yeezy