Gini-Koeffizient für Ligen
In der Ökonomie beschreibt der Gini-Koeffizient die Ungleichheit einer Einkommensverteilung in der Bevölkerung. Wir wollen den Gini-Koeffizienten auf Liga-Tabellen anwenden und als Einkommen die Liga-Punkte $P_n$ der $n=1,...,N$ Teams verwenden. Bei der Anwendung auf Liga-Tabellen gibt es Besonderheiten zu berücksichtigen. Zum einen ist die Größe $N$ eine kleine Zahl im Bereich von $N\simeq 10-20$, zum anderen ist das minimale und maximale Gesamteinkommen eindeutig festgelegt. Des Weiteren können bedingt durch die Regeln der Punktevergabe nicht alle Punkteverteilungen realisiert werden.
Auf diese Aspekte wollen wir im Folgenden eingehen und beginnen mit der klassischen Definition des Gini-Koeffizienten.
Definition des Gini-Koeffizient
Die Definition des Gini-Koeffizient $G_N$ ist gegeben durch:
$$
{\cal{P}}:=\{P_1,...,P_N\} \quad \mapsto \quad
G_N({\cal{P}}) := \frac{\sum\limits_{n=1}^N\sum\limits_{m=1}^N | P_n-P_m|}{2N^2 \langle {\cal{P}} \rangle},
\qquad
\langle {\cal{P}} \rangle = \frac{1}{N}\sum_{n=1}^N P_n,
$$
wobei ${\cal{P}}$ eine Verteilung von Einkommen $P_n\geq 0$ der $N$ Spezies ist, die mit $n=1,...,N$ indiziert sind. Wir wollen diesen Koeffizienten auf den spezifischen Fall von Ligen mit $N$ Mannschaften anwenden. Dabei ist das Einkommen die Zahl der Punkte, die ein Team in einer Saison erzielt. Damit gibt es eine Tabelle für die eine Ordnung der Form: $P_n \geq P_m,\; \forall 1 \leq n<m \leq N$ existiert. Mit dieser Ordnung kann der Gini-Koeffizient geschrieben werden als:
$$
G_N({\cal{P}}) = \frac{1}{N^2\langle{\cal{P}}\rangle}\sum_{n=1}^N(N+1-2n)P_n.
$$
Diese Darstellung ist der Ausgangspunkt der folgenden Betrachtungen. Schauen wir uns zunächst die klassischen EIgenschaften an.
Eigenschaften des Gini-Koeffizienten
Die für die Interpretation wichtigen Eigenschaften sind:
Semipositivität $$ G_N({\cal{P}}) \geq 0, \quad \forall {\cal{P}} $$ Gleichverteilung $$ {\cal{P}}_{min} = \{P_1=P_2=...=P_N=p\} \qquad \Rightarrow \qquad G_N({\cal{P}}_{min}) = 0 $$ Maximale Ungleichverteilung $$ {\cal{P}}_{max} = \{P_1=p, P_2=...=P_N=0\} \qquad \Rightarrow \qquad G_N({\cal{P}}_{max}) = 1 - \frac{1}{N} $$ Damit gilt: $0\leq G_N({\cal{P}}) <1$. Ist das Einkommen unter allen Teilnehmern gleichverteilt, so ist $G_N=0$, ist das Einkommen maximal ungleich verteilt, so ist $G_N=1-1/N$ maximal. In einer Liga ist ${\cal{P}}_{max}$ jedoch nicht realisierbar. Deswegen betrachten wir zunächst die Besonderheiten von Punkteverteilungen in Ligen, bei der $p_s$ Punkte für einen Sieg und $p_u$ Punkte für ein Unentschieden vergeben werden. Wir werden hier nur den Fall $p_s=3$ und $p_u=1$ betrachten, alle Rechnungen können aber auch allgemein durchgeführt werden.
Punkteverteilungen in Ligen
Die Frage ist: Wie sieht die Punkteverteilung $\hat{\cal{P}}$ aus, die $G_N({\cal{P}})$ maximiert? Die Beantwortung dieser Frage ist nicht trivial und ebenso die allgemeine Beweisführung, auf die wir an dieser Stelle verzichten. Stattdessen betrachten wir eine Serie von Punkteverteilungen in der Form:
$$
{\cal{P}}_\ell := \{P_1=6(N-1),P_2=6(N-2),...,P_\ell=6(N-\ell),P_{\ell+1}=...=P_N=2(N-\ell-1)\}
$$
für $\ell=0,...,N-1$. Diese Serie enthält mit ${\cal{P}}_0={\cal{P}}_{min}$ die Gleichverteilung und mit ${\cal{P}}_1$ die Verteilung, bei der ein Team alle Spiele gewinnt und $6(N-1)$ Punkte holt und alle anderen Teams die gleiche minimale Punktzahl $2(N-2)$, sodass gilt:
$$
{\cal{P}}_{1} := \{6(N-1),2(N-2),....,2(N-2)\}
\qquad \Rightarrow\qquad
G_N({\cal{P}}_{1}) = \frac{2N-1}{N(N+1)}.
$$
Die Verteilung ${\cal{P}}_ {N-1}$ ist die, bei der ein Team alle Spiele gewinnt, ein zweites alle bis auf die 2 Spiele gegen das erste Team, das dritte gewinnt alle Spiele bis auf die gegen die ersten beiden Teams usw., dann gilt:
$$
{\cal{P}}_{N-1} :=\{P_n = 6(N-n),\;n=1,...,N\}
\qquad \Rightarrow \qquad
G_N({\cal{P}}_{N-1}) = \frac{N+1}{3N}.
$$
Im Allgemeinen gilt die geschlossene Form:
$$
G_N({\cal{P}}_{\ell}) = \frac{\ell}{N}\frac{4N^2-5N\ell+2\ell^2-N+l-1}{2N^2+2N\ell-\ell^2-2N-\ell}.
$$
Für ein festes $N$ gibt es ein $\ell=\ell_N$, für das gilt:
$$
G_N({\cal{P}}_{1}) < G_N({\cal{P}}_{2}) < ... < G_N({\cal{P}}_{\ell_N})
$$
$$
G_N({\cal{P}}_{\ell_N}) > G_N({\cal{P}}_{\ell_N+1}) > ... > G_N({\cal{P}}_{N-1}).
$$
Der maximale Gini-Koeffizient in Ligen
Conjecture
Der maximalen Gini-Koeffizient $G_N^{max}:=\max_{{\cal{P}}}G_N({\cal{P}})$ ist gegeben durch die Verteilung ${\cal{P}}_{\ell_N}$ mit $\ell_N=N/2+1$, so dass gilt: $$ G_N^{max} = G_N({\cal{P}}_{N/2+1}) = \frac{4N^3+N^2-10N+8}{11N^3-6N^2-8N}. $$
Für $N=18,20$ gilt dann explizit:
$$
G_{18}^{max}=\frac{2935}{7758}=0.378319...
\qquad\wedge\qquad
G_{20}^{max}=\frac{671}{1780}=0.376966....
$$
Liga-Koeffizient
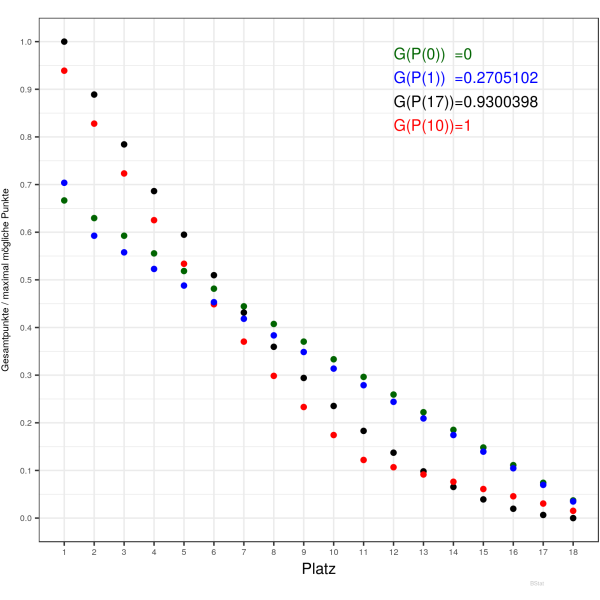
Da der maximale Gini-Koeffizient deutlich unterhalb von 1 liegt, definieren wir den normierten Gini-Koeffizienten: $$ \hat{G}_N({\cal{P}}) := \frac{G_N({\cal{P}})}{G_N^{max}}, $$ für den dann gilt: $0 \leq \hat{G}_N({\cal{P}}) \leq 1$. In den beiden folgenden Grafiken sind Beispiele von Gini-Einkommensverteilungen dargestellt. Hierbei ist darauf zu achten, dass die Auftragung zur gewöhnlichen Darstellung gespiegelt ist, damit die Tabellen Rangfolge von links nach rechts geht. Des Weiteren ist die Gesamteinkommens-Achse, normiert auf die maximale Anzahl der möglichen Punkte ($3(N-1)N$) einer Liga. Dies entspricht lediglich einer Skalenänderung und hat keinerlei Einfluss auf den $\hat{G}_N$-Wert. In den Grafiken ist jeweils für die verschiedenen Verteilungen der normierte Gini-Liga-Koeffizient $\hat{G}_N$ angegeben.
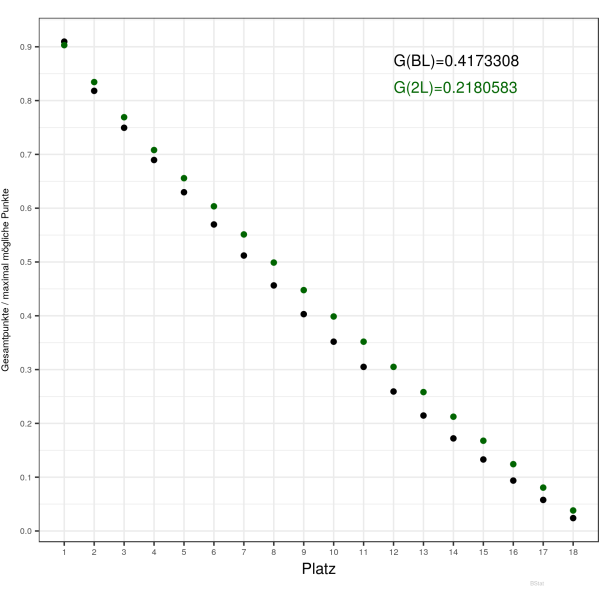
Die linke Grafik zeigt die oben diskutierten Verteilungen ${\cal{P}}_{0},{\cal{P}}_{1},{\cal{P}}_{N-1}$ und ${\cal{P}}_{N/2+1}$ für $N=18$. Die rechte Grafik zeigt den Verlauf der 1. und 2.Bundesliga für die Saison 17/18. Die zweite Liga war deutlich ausgeglichener, dies spiegelt sich in den $\hat{G}_N$-Werten von 0.417… zu 0.218… klar wieder.
An dieser Stelle sei noch bemerkt, die erreichte Gesamtpunktzahl $E:=N\langle {\cal{P}}\rangle$ geht in die Definition des Gini-Koeffizienten im Nenner ein. Für die oben diskutierten Verteilungen ${\cal{P}}_\ell$ variiert dies deutlich und ist der Mitgrund dafür, dass eine untypische Verteilung ${\cal{P}}_{N/2+1}$ existiert, die den Gini-Koeffizient maximiert. In der Praxis gibt es, wie auch in der rechten Grafik zu erkennen ist, eine nur sehr schwache Variation von $E$. Für die erste Liga lag der Wert in den letzten 6 zurückliegenden Spielzeiten bei $\langle E \rangle = 0.918 \pm 0.008$.
Fazit
Den normierten Gini-Liga-Koeffizienten $\hat{G}_N$ werden wir in weiteren Vergleichen von Ligen als Maß für die Ungleichheit der Liga verwenden, ob die Werte den subjektiven Einschätzungen entsprechen, muss dann gesehen werden.