Rangkorrelationen
Zur Quantifizierung von Zusammenhängen in geordneten Reihen kann man Rangkorrelationen verwenden. Wir betrachten hier den Spearmannschen Rangkorrelationskoeffizienten $r_s$ und wenden diesen auf Ligen mit $n$ Mannschaften an, die verschiedene Kennzahlen $t_i,p_i,...,x_i$, wie Tabellenplatz, Punkte, xGoals,… besitzen. Es seien $n$ Wertepaare $M:=\{(t_1,p_1),...,(t_n,p_n)\}$ gegeben, etwa Tabellenplatz oder Prognosen des Tabellenplatzes. Ordnet man solche Kennzahlen $t=(t_1,...,t_n)$ und $p=(p_1,...,p_n)$ der Mannschaften nach ihrer Größe, dann kann man die Ähnlichkeit beider Ordnungen durch eine Rangkorrelation vergleichen.
Wir bezeichnen die Abbildung $x_i\mapsto \mathsf{rg}(x_i)$, die die Kennzahl $x_i$ in einen Rang (Tabellenplatz) abbildet als Rangfunktion und ersetzen bei Ranggleichheit (Bindung) den Rang durch den Mittelwert der aufeinanderfolgenden Ränge.
Spearmann Rangkorrelationskoeffizient
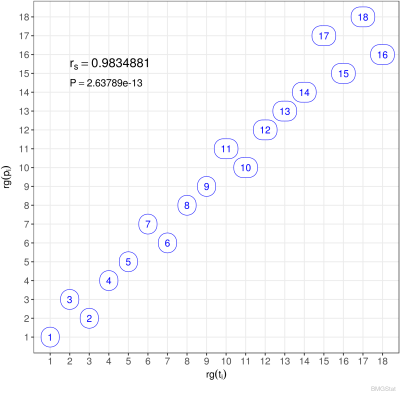
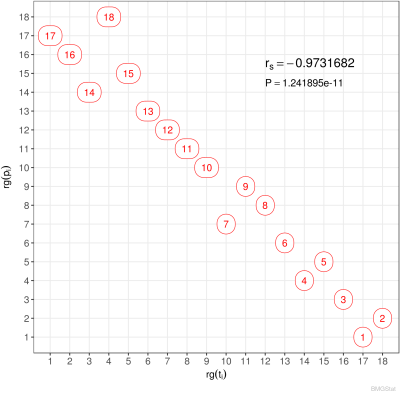
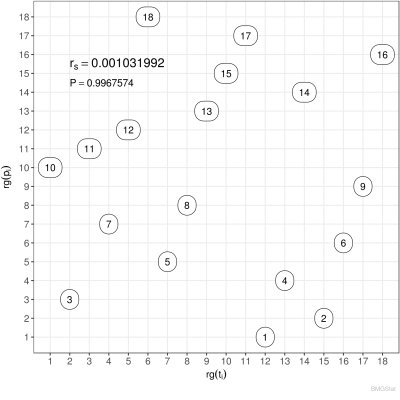
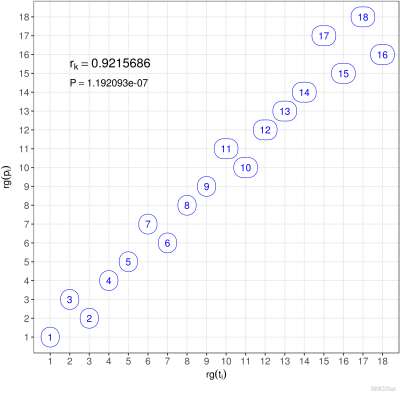
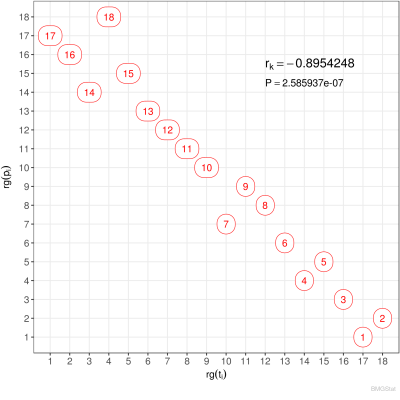
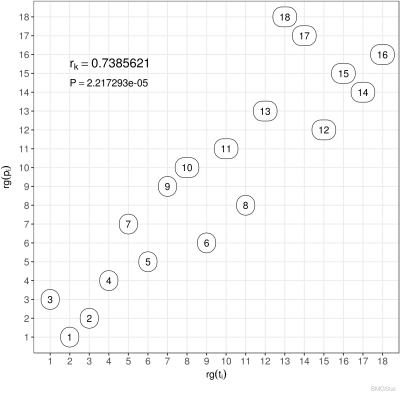
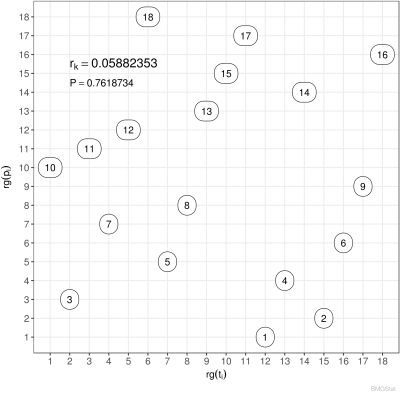
Der Spearmann Rangkorrelationskoeffizient der Paarmenge $M$ ist definiert durch: $$ r_s := \frac{\sum_i \big(\mathsf{rg}(t_i)-\langle\mathsf{rg}_t\rangle\big) \big(\mathsf{rg}(p_i)-\langle\mathsf{rg}_p\rangle\big)} {\sqrt{\sum_i\big(\mathsf{rg}(t_i)-\langle\mathsf{rg_t}\rangle\big)^2}\sqrt{\sum_i\big(\mathsf{rg}(p_i)-\langle\mathsf{rg_p}\rangle\big)^2}} $$ wobei $$ \langle\mathsf{rg_t}\rangle = \frac{1}{n}\sum_i \mathsf{rg}(t_i) = \frac{n+1}{2} \qquad\wedge\qquad \langle\mathsf{rg_p}\rangle = \frac{1}{n}\sum_i \mathsf{rg}(p_i)= \frac{n+1}{2}, $$ die Rangmittelwerte darstellen. Bei Fehlen von Bindungen reduziert sich der Spearmannsche Rangkorrelationskoeffizient zu: $$ r_s = 1 - \frac{6}{n(n^2-1)}\sum_i\big(\mathsf{rg}(t_i)-\mathsf{rg}(p_i)\big)^2. $$ Sind die Ränge beider Kennzahlen gleich $\mathsf{rg}(t_i)=\mathsf{rg}(p_i)$, so sehen wir, dass $r_s=1$, also maximal wird. Für eine Antikorrelation, bei der der erste Rang der ersten Kennzahl dem letzten Rang der zweiten Kennzahl entspricht, der zweite Rang der ersten Kennzahl dem vorletzten Rang der zweiten Kennzahl usw entspricht, es also gilt $\mathsf{rg}(t_i)=n+1-\mathsf{rg}(p_i)$, folgt: $$ r_s = 1 - \frac{6}{n(n^2-1)}\Big(4\sum_i \mathsf{rg}^2(t_i)-4(n+1)\sum_i \mathsf{rg}(t_i)+n(n+1)^2\Big) = 1 - \frac{4(n+1)(2n+1)-6(n+1)^2}{n^2-1}= -1, $$ Dies ist der minimal mögliche Wert. Gibt es keine Korrelation, so ist $r_s=0$. Beispielhaft sind hoch korrelierte Ordnungen ($r_s \lesssim 1$), unkorrelierte Ordnungen ($r_s \sim 0$) und antikorrelierte Ordnungen ($ r_s \gtrsim -1$) in den nachfolgenden Diagrammen grafisch dargestellt.
Statistische Signifikanz
Eine gründliche Diskussion der statistischen Signifikanz ist länglich und für unsere Zwecke hier nicht möglich. Wir werden lediglich in den Ergebnissen den P-Wert angeben, so wie in den Beispielen oben dargestellt. Desto geringer der $P$-Wert ist, desto sicherer können wir uns sein, dass die Ordnung nicht zufällig korreliert ist.
Ranggleichheit
Wir wollen den Rangkorrelationskoeffizienten in erster Linie für die Güte verschiedener Saison-Prognose verwenden. Hier ergibt sich die Besonderheit, dass in der 1.Bundesliga in der Prognose der FC Bayern München zu 100% von allen auf Platz 1 prognostiziert wird. Deswegen ist es interessant zu sehen, wie sich dies auf die Rangkorrelation auswirkt. Nehmen wir an $\hat{r}_s$ ist der Rangkorrelationskoeffizient für den Fall, dass für ein $i$ gilt $\mathsf{rg}(t_i)=\mathsf{rg}(p_i)=1$ und man nur noch $n-1$ Ränge besitzt, dann folgt für $n>2$: $$ \hat{r}_s = 1-\frac{6}{n(n-1)(n-2)}\sum_i \big(\mathsf{rg}(t_i)-\mathsf{rg}(p_i)\big)^2 = r_s - \frac{3}{n-2}(1-r_s) \leq r_s. $$ Die absolute Korrelation wird verständlicherweise kleiner, da ein Rang mit Übereinstimmung aus der Ordnung entfernt wird. Aber es ist zu beachten, dass desto größer der ursprüngliche Rangkorrelationskoeffizient $r_s$ war, desto weniger wird $\hat{r}_s$ kleiner werden. Das heißt, hohe Rangkorrelationen verlieren weniger.
Kendall Rangkorrelationskoeffizient (ohne Bindung)
Zum Vergleich betrachten wir den Kendall Rangkorrelationskoeffizient (ohne Bindung), der definiert ist durch: $$ r_k := \frac{N_k-N_d}{N_k+N_d} = \frac{N_k-N_d}{n(n-1)/2} $$ wobei $$ N_k := |\{(t_i,p_i) |\; t_i<t_j \quad\wedge\quad p_i < p_j \;\} |, \qquad N_d := |\{(t_i,p_i) |\; t_i<t_j \quad\wedge\quad p_i > p_j \;\} |. $$ Die Zahl $N_k$ ist die Anzahl der konkordanten Paare und $N_d$ die Anzahl der diskordanten Paare. Damit wird nicht der Abstand zwischen $t_i$ und $p_i$ berücksichtigt, sondern lediglich die Rangfolge der Paare.
Typischerweise ist $r_k$ kleiner als $r_s$, aber nicht rigoros, wie auch in den Vergleichen im Folgenden zu sehen ist.